
He is also an author for the upcoming O'Reilly book High Performance Images
TL;DR:
- bla, bla, bla, chroma, luma, color theory, human eyes, bla, bla, bla
- 60% of images don’t use chroma-subsampling; but 40% do use 4:2:0
- Subsampling is good for mobile: reduces bytes and saves memory on the device
- You can expect to reduce image size by ~17% by using Subsampling 4:2:0
- Recent advances in the sampling algorithms make it much safer to apply
- Bottom line: You should use 4:2:0 today. Your Ops team will love you, your marketing team will love you and your users will love you
- The world needs more love. Subsample 4:2:0 today
Intro
It has been 80 years since Alda Bedford’s “Mixed Highs” theory was proposed and yet over 60% of the images we download ignore his discovery. Alda’s theory is the root of Chroma-subsampling in video and particularly images. Chroma-Subsampling can reduce JPEG Image byte size by an additional ~17% and has the added benefit of also improving the rendering performance on the device by using less video memory. Unfortunately, most images on the web do not use subsampling.
Special thanks to: David Belson, Nick Doyle, Peter Rabinovich, Tim Kadlec, and Yoav Weiss.
Jump to:
- Chroma History 101
- Definitions
- Understanding Chroma-Subsampling notation
- 1 million image study
- Chroma subsampling in the wild
- Why not just universally use 4:2:0
- How much smaller could my images be with subsampling?
- Is the dataset comparing apples to apples?
- How much smaller are 4:2:0 images?
- Regression Analysis
- Correlation is not Causation !!!!!!
- Subsampling is getting better
- Conclusion
Chroma History 101
Back when dinosaurs roamed the earth, a team at RCA was wrestling with how to compress color television signal to only 6Mhz. Fortunately, Alda and team had realized that the human eye is a silly apparatus and can easily be tricked. Specifically, the eye is much more sensitive to changes in brightness than color. In this way you can reduce color detail so long as you keep the brightness detail. Even better, the faint glow of the TV tricks your eyes to think it is daylight so the gender difference of the density of rods and cones virtually becomes negligible.
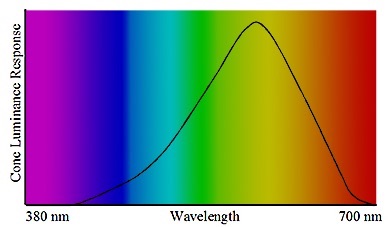
This is why green and blue can look the same sometimes – even to non colorblind eyes. Pro tip: never play strategy board games in low light to avoid accidentally confusing colors.
When the RCA team solved the NTSC over-the-air TV problem, they focused on splitting the Luma (brightness) and chroma (color) signal. This way an old black and white tv could work with just the brightness part and a color TV would overlay the brightness on top of the color. Perfect backward compatibility.
Fast forward to digital video recording. Again, we have the same problem of how to compress video data to fit on magnetic tape and broadcast. It is with digital video and HD that we see the increased use of subsampling. Now it is nearly ubiquitous in use for video. As you binge watch Jessica Jones, reflect how your non-superhero eyes are being tricked but helping deliver a superior video streaming experience.
Definitions
I’ll be honest, I’m intimidated every time I talk to someone about chroma-subsampling. Not just because the vowel to word-count is high, but because there are many terms and jargon used in the discussion and many of them almost interchangeably. Without a Fine-Arts degree it is understandable why it is easy to get lost. To help make sure we are all on the same page I’ll try and keep to a few definitions. And if I’m wrong, well, we’ll all be wrong together.
- Luma describes the lightness or darkness of a color. With just Luma, you would have a black and white image. In other words, while Instagram has convinced you that b&w photos are cool, the reality is really it allows them to save bytes per image.
- Chroma is only the color detail. Adding Luma to Chroma produces the color you expect. If you ever use the color picker in office or photoshop, you probably remember that you can select a color by RGB value or sometimes using Hue-Saturation-Brightness values. Functionally they are they result to the same thing and can be converted one to the other. Hue uses a color wheel and then you apply lightness and darkness (saturation and brightness) to the color.
Understanding Chroma-Subsampling notation
There are many nuances when it comes to expressing Chroma-Subsampling. There are several different notations and variations each with different histories. The most common notation is J:a:b and usual values are 4:4:4 or 4:2:0.
The JPEG notation (exposed by ImageMagick for example) is a little difficult to understand. It uses a H1xV1,H2xV2,H3xV3 notation. For quick reference:
4:4:4===1x1,1x1,1x14:2:0===2x2,1x1,1x1
Fundamentally, this notation expresses how to sample just the color while leaving the luma intact. You can read it like this: Given 4 pixels wide (J), how many unique unique color-pixels in row 1, and row 2 should be used. In this way:
- 4:4:4 use 4 unique pixels on the first row, and 4 unique on the second.
- 4:2:0 means use 2 unique pixels (every other entry) and use the same value on the second row as below

This can reduce the amount of data in an image. Put another way:

The result is that luma and chroma details become greatly simplified in the JPEG byte stream. For a 4:2:0 subsampling, it will functionally look like this:
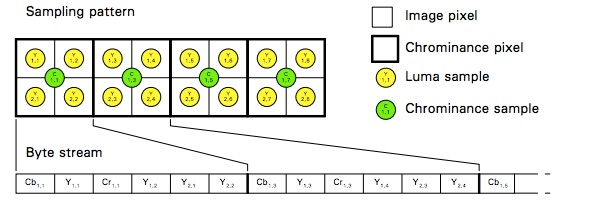
Don’t worry if this isn’t entirely clear. It is a bit of a twister for the brain. If you want to learn more about the notation and the variations I would suggest the following resources:
- http://www.videomaker.com/article/f6/15788-the-anatomy-of-chroma-subsampling
- http://photo.net/learn/jpeg/#chrom
- http://dougkerr.net/Pumpkin/articles/Subsampling.pdf
- http://wolfcrow.com/blog/chroma-subsampling-numbers-explained/
1 million image study
If Chroma-Subsampling is such an old science, I wanted to understand how well it is used in the wild. Some photo editing programs, such as imagemagick, default to use 4:2:0 based on quality settings or other heuristics. Yet, there are many different variations in subsampling rates and each with its own subtle nuances.
To answer this question, I wanted to use the top 1 million images accessed by users. One option is to use the Alexa top 1000 much like HttpArchive.org does. But this only tells us which sites are most used, not necessarily which images are hit the most. It also is very NorthAmerica centric. In the end I decided to use a dataset from my employer, Akamai. I selected the top 1 million JPEG images accessed by end users, with an equal weighting and distribution for geography and business.
[Side note: sorry, I can’t directly publish the image set. Our legal teams have concerns about rights to digital content and disclosing customer lists]
Chroma subsampling in the wild
From this image set, I ran an analysis on each image to determine the characteristics of each image. The simplest way to do this is to use imagemagick’s identify tool. (you can also use exiftool, but identify allows me to format the output for later user)
identify -f "%[jpeg:sampling-factor]" images/0c/90/f85bb0bcbc2e012faffde9ae4481.jpg
This will yield a result like: 1x1,1x1,1x1 or 2x2,1x1,1x1. ImageMagick uses JPEG’s funny notation for subsampling with a number of redundant variations. A deeper explanation can be found on page 9 of Doug Kerr’s Chroma Subsampling in Digital Images. It also includes a good reference table to convert the H1xV1,H2xV2,H3xV3 notation to J:a:b.
Running this against the JPEG dataset has the following results:
| Subsampling (J:a:b) | Count | Percent | | ------------------- | ------- | ------- | | 1x1 (b&w) | 2460 | 0.2% | | 1x1,1x1,1x1 (4:4:4) | 596,370 | 59.7% | | 1x2,1x1,1x1 (4:4:0) | 544 | 0.1% | | 1x2,1x2,1x2 (4:4:4) | 242 | 0.0% | | 2x1 (b&w) | 29 | 0.0% | | 2x1,1x1,1x1 (4:2:2) | 6403 | 0.6% | | 2x2 (b&w) | 42 | 0.0% | | 2x2,1x1,1x1 (4:2:0) | 393,192 | 39.3% | | 2x2,1x2,1x2 (4:2:2) | 294 | 0.0% | | 2x3,1x1,1x1 (whaa?) | 1 | 0.0% | | 4x1,1x1,1x1 (4:1:1) | 163 | 0.0% |
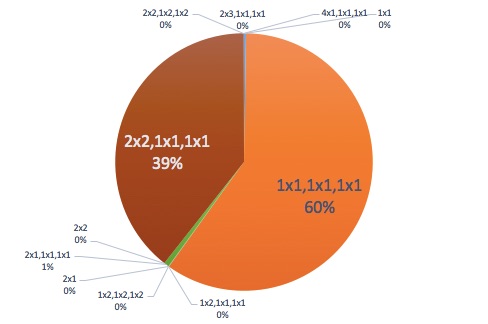
This implies that only 40% of all JPEG images use any kind of subsampling. Most of which are 4:2:0. Visual inspection of the other varieties of subsampling (such as 4:4:0 and 4:1:1) revealed that these images appeared to derive from video sources such as a thumbnail for a video stream or a game. Likely this is the result of an MPEG2 frame being sliced out and the original video being encoded with the other subsampling variants.
Interestingly there are some odd sampling rates in this data. Many of them don’t make a lot of sense. 1×1 (and also 2×1, and 2×2) are grey scale images without any chroma. 2×3,1×1,1×1 is the most curious of the lot. Clearly it is an outlier but what is it? The only reference I could find was from an old version of PaintShopPro. Worse yet, it was a new image, created in the last month. Old tools take a long time to be expunged from the ecosystem.
Why not just universally use 4:2:0?
Clearly 4:2:0 is the most popular. As I mentioned above, this is do to many of the popular tools defaulting to 4:2:0 and video broadcast standards. Any transformations, resizes,etc done through an image farm will likely result in this subsampling.
WebP also only uses 4:2:0. This is more of a function of VP8 exclusively supporting 4:2:0 and no other sampling rate. If you convert to WebP you cannot use any other sampling rate.
If it is so great, why don’t we force 4:2:0 on all images? A couple of key issues:
- Tools. Not all tools offer this technique and many that exist get it wrong.
- Many tools can distort some images because the subsampling is ‘ineffective’. Which, in this context, is a polite way of saying that not all smart people are made equal.
The most pervasive issue is that when you are sampling the color of a block of pixels you can run into issues where there is a hard line with high contrast. Take for example the imagemagick logo. The red letters suddenly have a dark red outline. More pronounced examples can be found on Kornel’s Jpeg Compressor Example.


As a result, many tools and teams have created a blanket policy of no-subsampling so as to avoid these edge cases. Unless you are willing to evaluate each image, the thinking goes, you should avoid subsampling. Of course, you could say that about using compression 80%, or resizing. (More on this in at the end.)
But why don’t more people notice this in video when we use subsampling 4:2:0? The short answer is it is because it is motion and the brain doesn’t have time to notice undesirable artifacts.
How much smaller could my images be with subsampling?
What’s all the hullabaloo? If 4:2:0 has some edge cases, then why should you even bother? Two main reasons:
- Reduce device memory for images. This is particularly pertinent for mobile devices.
- Smaller file sizes thus improved performance on the network.
Smaller images are good. But how much smaller? The challenge is claiming a precise decrease in bytes without also taking into consideration other factors that could contribute, particularly compression.
The obvious choice is to force 4:2:0 compression on all the images that were previously 4:4:4. Unfortunately we don’t have the original image. Any changes to the subsampling will cause the image to be re-encoded and thereby likely change the quantization tables used for recompression. We will no longer be measuring the effect of subsampling, but rather the effect of decompressing, subsampling and recompression. This is a dubious process; it won’t be a clean conversion.
The better path is an observational study that uses regression analysis using the million sample images. What can we learn from comparing 4:4:4 to 4:2:0 images, of which there are about 550k and 450k of each respectively? Can we determine what factors more greatly impact the output bytes: dimensions, compression and subsampling? The answer is yes.
Is the dataset comparing apples to apples?
With an observational study, the biggest question is whether we are really comparing like with like.We want to make sure that we aren’t doing something silly like grouping lego bricks by color and then measuring the nutritional value. We want to make sure that the group of images that are 4:4:4 have the same range of characteristics as 4:2:0. For example, maybe 4:2:0 are mostly beacons and 4:4:4 are product images.
First, let us compare the pixels displayed. A quick survey shows they look like they have similar distributions:
| J:a:b | Median(dimensions) | Median(Bytes) | Median(Compression) | | ----- | ------------------ | ------------- | ------------------- | | 4:4:4 | 300x200 | 9.3KB | 94 | | 4:2:0 | 280x208 | 14.9KB | 84 |
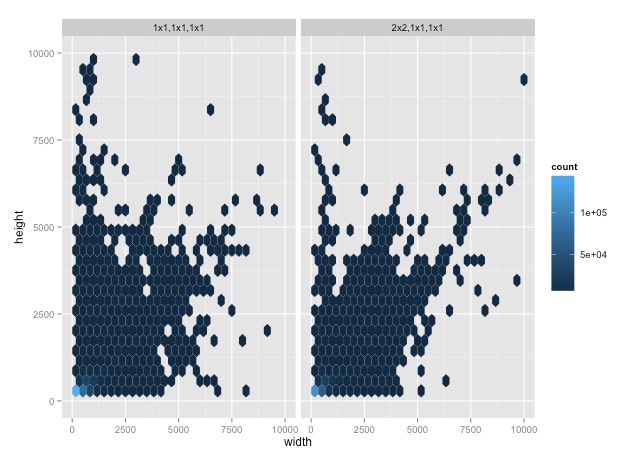
From a pixel perspective, they seem to have the same kinds of shape. That is, the mean number of pixels is around 250,000 (500×500). Though it is sad that so few images show off the glory of our giant phablets, we can be encouraged that perhaps this dataset is pretty representative.
While compression is hardly canonical and consistent, we should compare the use of these labels to pixel volume:
![]()
So far, they look fairly similar.
Finally, a visual inspection of the images shows that there is a wide range of usages and content.


How much smaller are 4:2:0 images?
Now that we’re reasonably convinced that we are looking at the same kind of images, we can start to answer the question of impact. That is, given an average JPEG image, how much of an impact would you expect? Are compression algorithms already realizing much of the same gains that subsampling would bring?
A visual survey of the data with a scatter plot of bytes and pixels (width*height) seems to suggest that yes, 4:2:0 images tend to have few bytes (up and to the left). More specifically, it does appear to become more pronounced as you increase the pixels. But I’m still using my brains’ fuzzy pattern detector.
![]()
Regression Analysis
Using a regression analysis, we can help explain how subsampling is related to prove this out. Don’t feel bad if it has been awhile since university. In reality, people just use ‘regression analysis’ as a pick up line. (or maybe it was when you are about to be dumped?) In reality, no one really knows how to do calculations by hand: we just let our subservient computers do the work.
The short summary is that a regression will help us figure out how much different factors impact the byte size of a JPEG. Looking at the dataset here, we’ll focus on image quality (compression), total pixels, subsampling rate and output bytes. I’m not including progressive, color pallet, and a few other possible factors because a cursory evaluation showed that they weren’t as strongly impactful. That, and I ran into issues identifying progressive images that I couldn’t resolve before publishing.
## Call: ## lm(formula = logbytes ~ logpixels + compression + subsampling, data = data) ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) -1.002e+00 8.574e-03 -116.8 <2e-16 *** ## logpixels 6.801e-01 3.796e-04 1791.4 <2e-16 *** ## compression 4.076e-02 7.665e-05 531.8 <2e-16 *** ## subsampling 2x2,1x1,1x1 -1.867e-01 1.550e-03 -120.5 <2e-16 *** ## --- ## Signif. codes: 0 '**' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.6826 on 989558 degrees of freedom ## Multiple R-squared: 0.7775, Adjusted R-squared: 0.7775
Do your eyes hurt?
For 78% of the data points, we can explain the size of bytes using this equation:
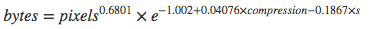
where s=1 if the subsampling scheme is 4:2:0, and 0 otherwise. This is equivalent to:
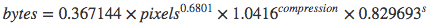
Specifically:
- resizing images matters most. It multiplies the size a little more than the square root of the total pixels. More pixels, many more bytes.
- compression matters somewhat. For quality=80 the bytes are x23; for quality=100 bytes multiply x50.
- subsampling of 4:2:0 could further reduce the bytes by 17%
Put another way: We would expect 17% byte savings from using 4:2:0 subsampling compared to no subsampling.
Correlation is not Causation !!!!!!
Fine. What if this observational study is just correlation caused by the adoption of JpegTran and its better quantization tables?
To counter this, I did do a test by converting the 4:4:4 images to 4:2:0 images. Again, let me stress that by doing this we risk the Hawthorne effect (observer effect). Images that are used in the wild represent a state that has been QA'ed and validated as good. Blindly converting the subsampling doesn't account for this.
If you have made it this far down in the post and want to try this at home, here is the command I used:
convert in.jpg -sampling-factor "2x2,1x1,1x1" out.jpg
Comparing the before and after yielded the following result. This plot shows the distribution of gain (% improvement) against pixel count:
![]()
In this, the median gain is 17% and the average is 19%! Despite my reservations, converting the dataset does show that over 50% of the time you should see 17% reduction in byte size - or more!
Subsampling is getting better
As I mentioned above, the most common sub-sampling algorithms can cause some distortion especially when encountering high contrast straight lines. The good news is that there has been a lot of work on this recently. Kornel Lesiński has authored a great library to do better at subsampling and the WebP team has recently update the sampling algorithm that hopefully could be brought back to jpeg.
Conclusion
Subsampling is a jargon filled subject matter and, quite frankly, can be intimidating. That said, you will look like a pro to your boss when you convert your images to use Chroma-Subsampling of 4:2:0. Not only will you reduce the device memory - especially important on mobile devices - but you will also reduce the bytes transferred by ~17%. Your network and infrastructure teams will love you for helping them save disk space and reduce network utilization. Marketing will love you because they will have permissions to use larger images. But best of all, your users will love you because you'll have a faster website!
The world needs more love. Subsample today.
